困惑数学大师们358年的谜题——费马大定理艰辛证明之路
费马大定理的提出
17世纪初,欧洲流传着公元三世纪古希腊数学家丢番图所写的《算术》一书。大约在1637年前后,法国数学家费马在丢番图的《算术》的第二卷关于毕达哥拉斯三元组的页边上,写下了一段结论“不可能将一个立方数写成两个立方数的和;或者将一个4次幂写成两个4次幂之和;或者,更一般的说,不可能将一个高于2次的幂写成两个同次幂的和”。接着,他又俏皮地写下一个附加的评注:“我对此命题有一个十分美妙的证明,只是这里空白太小,写不下”。上述评注是费马死后5年的1670年发表的。人们称上述问题为“费马大定理”。简单说,费马大定理就是n≥3时,下面不定方程没有正整数解。
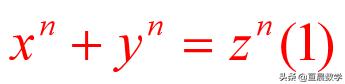
费马的附加评注让当时的很多数学大咖困惑,既然存在美妙证明,那就证呗,可这看似简单的问题却无人能给出证明。于是开始搜寻费马的美妙证明方法,人们遍寻费马的手迹,并没有发现这一美妙的证明,不过,也有所收获,找到了他对于n=4的证明,下图是大学数学教材初等数论中给出的费马关于n=4证明的方法,一般中学生都能看懂,费马对这一证明颇为得意,称之为“无穷下降法”。

费马关于n=4的证明方法
或许费马认为用这种方法可以证明任意n≥3时的情形,但事实却不是那么简单,因此只能认为上述结论是猜想,后来很多数学家以及民间数学爱好者都试图证明该结论,却都以失败告终。以至于除了它以外,费马提出的其它猜想早已得到解决。
费马

费马
皮耶·德·费马是17世纪法国律师,也是一位业余数学家。之所以称业余,是由于费马具有律师的全职工作。。著名的数学史学家贝尔在20世纪初所撰写的著作中,称费马为”业余数学家之王“。贝尔深信,费马比同时代的大多数专业数学家更有成就。
漫长曲折无果的求证之路
由费马的n=4证明可知,如果能够证明对于任意奇质数p来说,(1)式没有正整数解,那么对p的任一倍数n来说,(1)式也没有整数解,而费马问题也就完全解决了,但谈何容易。费马的猜想提出一百年后,欧拉大约在1753年至1770年之间才运用代数整数环的性质证明了p=3的情形,而且欧拉的证明过程也有漏洞,不过这个漏洞由勒让德补充了。勒让德和狄利克雷分别于1825年和1828年独立地证明了p=5的情形,拉梅于1839年证明了p=7的情形。

欧拉
在19世纪,对费马大定理的证明作出最大贡献的非库默尔莫属。
1884年,库默尔证明了若(2)具有唯一分解性,则费马大定理对P具有成立,并用统一方法验证得到p≤19成立。
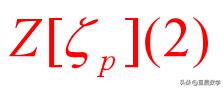
1847年至1851年库默尔又发明了一种“理想数”,用“理想数”的唯一分解性使得费马大定理的证明获得重大突破。他建立正规数的一种判别方法,验证了p≤100中,除了37,59,67外都是正规数。他又采用进一步方法,证明了费马大定理对p=37,59,67也成立。但他的证明也有漏洞,不过后来被人补上。由此费马大定理对p≤100成立。

库默尔
希尔伯特在1900年世界数学家大会上谈到研究数学问题的重要性时,有如下一段论述:受费马问题的启发,库默尔引进了理想数,并发现了把分圆域的理想数分解为理想质数的惟一分解定理,这个定理今天已经被戴德金和克罗内克推广到任意代数领域,在近代数论中占着中心地位,其意义已经远远超出数论的范围而深入到代数和函数论的领域。足见对库默尔研究的肯定。
从库默尔以后至20世纪70年代,人们继续研究费马大定理对于更大质数的成立,到1976年,已经知道,费马大定理对于小于125000的质数成立。可是,实事求是说,这些研究没有本质的进展。人们完全看不到解决费马大定理的任何希望。甚至有人预言,这个问题本世纪是不可能得到解决的。但是,希望总是在最绝望时出现。
“山重水复疑无路,柳暗花明又一村”
1983年德国青年数学家法廷斯结合使用了苏联和美国哈弗两个代数几何学派的工作,证明了莫代尔猜想。
莫代尔猜想:如果有理系数的多项式方程Q(x,y)=0定义的曲线的亏格≥2,则此方程只有有限多个有理数解。
法廷斯在证明过程中,使用了20世纪50年代以来发展的现代代数几何工具。莫代尔猜想尽管不能直接解决费马大定理,但它向人们提供了另外一条路向其靠近,而且有希望从代数几何方面获得解决费马大定理的有力工具。
现在开始故事的转折部分,在德国的一个小镇,多年来,这里成为世界各地数学家的“旅游区”。每年会举办数学问题的高级研讨会,交流数学成果和思想。1984年秋,一群优秀的数论学家聚会,讨论关于椭圆曲线的各种突破性工作。德国数学家弗雷演讲中提到一条椭圆曲线方程——弗雷曲线,然后他推导出这条曲线不满足关于椭圆曲线的谷山-志村-韦依(TSW)猜想.也就是说,如果费马大定理不成立,那么著名的TSW猜想也不成立。即由TSW猜想可以推出费马大定理。
TSW猜想:Q(有理数)上的每条曲线都是模曲线
在弗雷演讲的时候,所有的在场观众都发现其中有个明显的逻辑错误,每个人都想补救这一缺陷,但没人做得到,问题太难了,直到1986年世界数学家大会期间,弗雷演讲的两位听众里贝特和梅祖尔,前者向后者讲述他两年来完善弗雷演讲缺陷的方法和遇到的困难,没想到后者的提示让其很快完成了证明弗雷论断的工作。
于是证明费马大定理的工作变成了证明TSW猜想,甚至只要对弗雷曲线证明证明TSW猜想成立即可,但当时许多数学家认为这依然困难,里贝特本人也持悲观态度。但怀而斯坚信可以。
怀而斯在当时已经成长为数论,椭圆曲线和模型式方面成熟而杰出的青年数学家。他自忖:“当然,已经很多年了,TSW一直没有解决,没有人对怎样处理它有任何想法,但至少它属于数学的主流,……,我不认为我在浪费自己的时间,这样,吸引我一生的的费马传奇故事和一个专业上有用的问题结合起来了”。怀而斯下决心研究TSW猜想。从那时起的7年,他除了教书,指导研究生和参加必要的研讨以外,放弃了所有与证明TSW猜想无关的研究工作,躲在家中一心一意研究TSW猜想。他不与任何人讨论,也不发表任何部分结果,反而为了掩人耳目,时不时发表一些小论文。甚至与他关系密切的同事也没注意到他的研究所在。他的老师也毫不知情。

怀而斯
在怀而斯研究之初,1988年他读到了报纸上宣称东京大学的宫冈洋证明了费马大定理。不过最后发现了逻辑上的错误,一批数论学者试图补救也无济于事。这一场虚假证明使怀而斯虚惊一场。
1990年,怀而斯开始研究究岩泽理论来寻找突破,但到1991年仍然毫无结果,他认为归隐5年而无结果,应该重返学术交流圈以便了解新的学术成果。他参加了波士顿举行的椭圆曲线会议。在这个会议上,他的老师科茨告诉他,一位叫弗莱切的学生用科利瓦金的方法研究椭圆曲线。怀而斯意识到这个方法很适合他,但这涉及到一些他不熟悉的问题,为了保证证明的正确性,他向同事凯兹寻求帮助。终于在1993年,他确信证明已经完成。6月在剑桥举行“L—函数和算术”学术会议,会议的组织者之一,他的老师科茨应他请求,破例为他安排了题为“模形式、椭圆曲线和伽罗瓦表示”的三次演讲。他的演讲只字不提费马猜想,最后一句:“这样我就对所有半稳定椭圆曲线证明了TSW猜想”。在场专家都知道,这是在宣布证明了费马大定理呀,会场立马沸腾。因为这次会议有中国数学家参会,会议当天国内就获得了此消息。
兴奋过后,开始了严格的审查,审查让人6位,每人负责审查一章,其中第三章的审查者凯兹发现了一个问题,起初怀而斯以为很容易补救,后来意识到困难重重。在各种压力下,1993年12月4日怀而斯向数学界发了一个电子邮件。大意是:发现很多问题,大部分已经解决,但有一个特别的问题没有解决,我相信我能解决。此时,他已经准备宣布失败,他的好友萨尔纳克建议他寻求帮助,怀而斯认真考虑后邀请他以前的学生,文章的审稿人之一泰勒来一起工作,但直到1994年夏仍没结果。这年8月,世界数学家大会在苏黎世召开,怀而斯与菲尔兹奖无缘。大会邀请了他作报告,他介绍了他的研究进展以及困难,大厅热烈的掌声是对他努力研究的肯定,这给了他很大鼓励。

菲尔兹奖
会后不久,一天早晨,他再一次寻找失败的原因,突然冒出一个想法,将岩泽理论和科利瓦金-弗莱切方法结合起来,果然情况如此,证明最后归结为一个纯代数问题。1994年10月25日两篇文章一起寄到了国际权威数学刊物《Annals of Mathematics》,一篇是怀而斯的《模椭圆曲线和费马大定理》,一篇是他与泰勒合作的《某些Hecke代数的环论性质》。文章于1995年发表。至此,一个困惑人间智者们358年的谜题终于揭开了。
1998年世界数学家大会授予怀而斯一个特别的菲尔兹奖(1994年他已经过40岁)
艰辛证明之路告诉我们:一个难题的解决需要创造新的方法,而这推动了数学的发展,后者比前者更重要。
