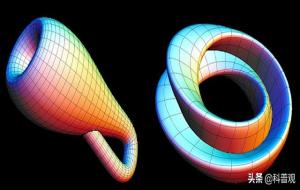克莱因瓶的原理是利用瓶颈通过弯曲穿过瓶子壁之后,瓶口直接和瓶的底部连接在一起,从而使这种瓶子没有内部与外部之分,成为了一种无定向性的平面,所以永远也装不满。
永远无法装满的克莱因瓶!据说来自四维空间,到底有多神奇?
科学界有很多理论假说没有办法被证明,我们相信它可以存在,却没有办法造出一个实物佐证它,其中最典型的就是克莱因瓶。
虽然当前市场上也有类似于克莱因瓶造型的容器,但却并不符合真正克莱因瓶的特性和存在要求,它于三维空间的我们而言只能是一个设想,你们知道这是为什么吗?
神奇的克莱因瓶
克莱因瓶其实是一个无定向边际的平面,它没有内外之分,允许物体从外部进去且不需要穿过瓶子。也就是说,克莱因瓶虽然存在曲面,但物体从任何一边的外面进去,都还是外面,这与三维空间的物体存在原理显然是相悖的。
而且实际存在的任何容器都是可以装满的,但是克莱因瓶却永远无法穷尽、无法装满,其中的缘由还得从它的假设提出说起。

克莱因瓶的发现
1882年,著名数学家菲利克斯·克莱因发现一个神奇的平面,将两个莫比乌斯环合二为一就可以得到,当时将其命名为“克莱因平面 ”,后因翻译原因才有了克莱因瓶的称呼。
莫比乌斯环相信大家都听说过,并且它也可以在现实生活中制作展示出来,就是一根纸带旋转180度再粘连,最后出现了一个只有单个平面的纸带。

而理论意义上,两个莫比乌斯环拼接在一起就会得到一个克莱因瓶,但如果不进行交叉重叠,这个设想是无法在三维空间中完成的。
从拓扑学的角度来看,克莱因瓶是个第四维的物体,由于人类相对四维空间来说属于低维生物,在我们的认知领域中只有长宽高,其余更高的空间结构即便真实存在,我们也无法看到。就像二维生物眼中没有高度,如果看到行进道路中有障碍物,二维生物也是无法跨过去的。在我们过往接触的数学理论中,由点到线、由线到面、由面到体的维度增加,都是可以被证明的,因为人类是三维生物,自然能够看到甚至解释低维事物。
可是没有人见过四维空间,根据一维、二维、三维的原理来说,四维也是无限个三维空间的叠加,所以如果四维物体存在于三维空间中,我们人类所看到的也只是它的投影。
克莱因瓶理论自提出以来,就引发了很多数学家的关注,许多人都认为,克莱因瓶可以覆盖整个宇宙,永远也装不满,这究竟又是为何呢?
克莱因瓶为何装不满?
首先,既然它是一个没有边界的平面,那么即便是容器形状也不具备容器的能力,可以置于空间之中却无法装满;其次,克莱因瓶底部有一个洞,但它的连接却并未穿过瓶子,这就像宇宙无穷无尽的原理一样,我们永远无法看到边界,也就不可能装满。

另外,克莱因瓶所处的四维空间于人类而言,还处在探索的初期,关于宇宙与各事物以及人类的存在意义,和从属关系,都还属于未知的状态。
但我们可以确定的是,克莱因瓶再一次打开了人类的视野,也许那些曾经的未解之谜同样是四维空间的故事,所有的真理都有可能在其他层面被推翻。
思考总结
克莱因瓶理论的提出丰富了拓扑学,为人类探索宇宙之谜创造了新的思维高度,也让我们不得不深思,当我们蹲在草丛中看着一群蚂蚁按部就班的寻找食物时,四维空间的生物是否也在俯瞰着我们呢?