芝诺悖论错在了时间上,这些悖论由于被记录在亚里士多德的《物理学》一书中而为后人所知,悖论之所以难以解决,是因为它集中强调后来笛卡尔和伽桑迪为代表的机械论的分歧点。
芝诺悖论(Zeno's paradox)是古希腊数学家芝诺(Zeno of Elea)提出的一系列关于运动的不可分割的哲学悖论
如果要行驶有限的距离,则首先必须行驶该距离的一半。如果你坚持将距离减半,你将需要无限的步,

根据古希腊传说,世界上跑的最快的人是女主人公亚特兰大。尽管她是一位著名的女猎手,但她以自己的速度而出名,因为没有人可以击败她。但是她还是古代哲学家伊莱亚·芝诺(Zeno)提出的许多类似悖论中的第一个的灵感:
为了从起点到目的地,亚特兰大必须先行进总距离的一半。要行驶剩余的距离,她必须先行驶剩下的一半。不管距离多小仍留下,她必须经过它的一半,然后一半的什么尚存,等等,循环往复。到达目的地所需的步骤无数,显然她永远无法完成旅程。因此,芝诺说,运动是不可能的:芝诺的悖论。这是不直观的解决方案
从最纯粹的数学角度出发,当然,您可能需要进行无限多次的跳转,但是每个新跳转都比前一个跳转越来越小。因此,只要您能证明需要进行的每次跳跃的总和加起来是一个有限值,那么将其分成多少个块就无关紧要。
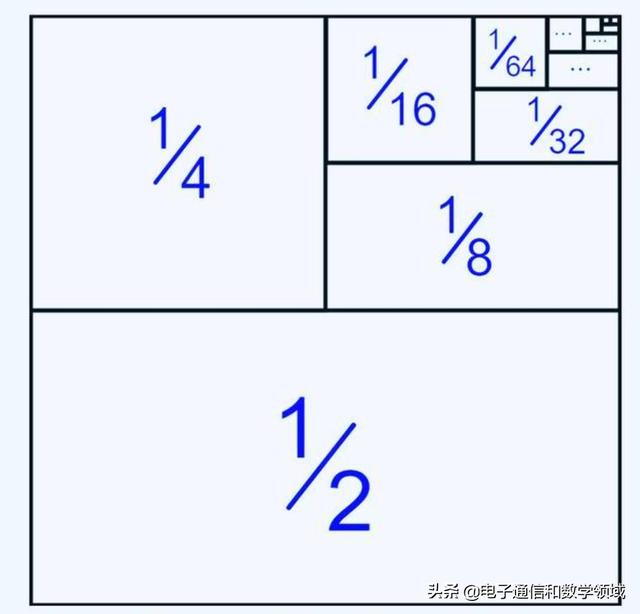
例如,如果将总行程定义为1个单位(无论该单位是什么单位),那么您可以通过将一半乘以一半乘以一半来到达那里,依此类推。系列+++ ...的确收敛为1,这样一来,如果您添加无限数量的字词,您就可以覆盖整个所需的距离。您可以通过从整个序列的两倍中减去整个序列来巧妙地证明这一点,如下所示:
- (系列)=+++ ..
- .2 *(系列)= 1 ++++ ...
- 因此,[2 *(系列)-(系列)] = 1 +(1/2 +++ ...)-(1/2 +++ ...)= 1。简单,直接和引人注目
但这也是有缺陷的。这种数学上的推理线仅足以表明您必须经过的总距离收敛到一个有限值。它并没有告诉您到达目的地需要多长时间,这是悖论中的棘手部分。
时间如何发挥作用,破坏这种对Zeno悖论的数学上优雅而引人注目的“解决方案”?
因为不能保证您需要进行的无数次跳跃中的每一个(即使跨越有限的距离)也会在有限的时间内发生。例如,如果每次跳跃花费相同的时间,无论走过多远,都将花费无穷的时间来掩盖剩下的微小旅程。在这种思路下,亚特兰大仍可能无法到达目的地。
许多古代和现代的思想家都试图通过援引时间观念来解决这一悖论。具体来说,正如阿基米德所断言的那样,完成较小的距离跳跃所需的时间要比完成较大的距离跳跃所需的时间短,因此,如果您行驶一段有限的距离,则必须只花费有限的时间。因此,如果是这样,亚特兰大终于可以到达目的地并完成旅程。
只是,这种思路也是有缺陷的。显然,完成每个步骤所需的时间仍然会减少:原始时间的一半,原始时间的三分之一,原始时间的四分之一,五分之一,等等,但是整个旅程将花费无限的时间。您可以通过尝试找出[1/2 ++++++ ...]的总和来自己检查一下。事实证明,这个限制并不存在:这是一个分歧的系列
如此处所示,调和级数是每个项均小于上一项的级数的经典示例,但是总级数仍然有所不同:即,总和趋于无穷大。仅仅争辩说随着距离的跳跃变短,时间的跳跃变短是不够的。定量关系是必要的
这似乎是违反直觉的,但是仅凭纯粹的数学并不能为悖论提供令人满意的解决方案。原因很简单:悖论不只是将有限的事物分成无数个部分,还在于速率的内在物理概念。
尽管通常仅根据距离来构成悖论,但悖论实际上是关于运动的,这大约是在特定时间内覆盖的距离量。希腊人用这个词来形容-τχο,这是我们从中获得“ tachometer”甚至“ tachyon”之类的现代词的地方,字面意思是事物的迅捷。但是,这个概念仅在质的意义上为人所知:距离与“ τχο ”(或速度)之间的明确关系需要通过时间进行物理连接

事物移动多快?那是速度。
加上它往哪个方向移动,就变成速度了。
与距离和时间有关的速度的定量定义是什么?它是距离的整体变化除以时间的整体变化。
这是一个称为比率的概念:一个量(距离)随另一个量(时间)而变化的量。您可以具有恒定速度(无加速度)或变化速度(有加速度)。您可以具有瞬时速度(您在某个特定时刻的速度)或平均速度(您在整个旅程的特定部分或整个过程中的速度)。
但是,如果某物处于恒定运动中,则距离,速度和时间之间的关系变得非常简单:距离=速度*时间。
这就是通常所说的经典“ Zeno悖论”的解决方案:对象可以在有限的时间内从一个位置移动到另一个位置(即,行进一段有限的距离)的原因是因为它们的速度不仅总是有限的,而且因为除非有外部力量对其采取行动,否则它们不会及时改变。如果您让一个像Atalanta这样的人以恒定的速度运动,那么她将在等式中提出的一定时间内覆盖任何距离,该等式将距离与速度相关联。
这基本上是牛顿的第一定律(静止的物体保持静止,运动的物体保持恒定运动,除非受到外力作用),但适用于恒定运动的特殊情况。如果您将行驶的距离减半,则只需花费一半的时间即可遍历。要穿越(+++ ...)想要覆盖的总距离,您需要花费 (+++ ...)的总时间。无论您有多小,它都可以覆盖任何距离。
对于任何对物理世界感兴趣的人,这足以解决芝诺的悖论。无论空间(和时间)是连续的还是离散的,它都有效。它在古典水平和量子水平上都起作用;它不依赖于哲学或逻辑假设。对于在此宇宙中移动的物体,物理学解决了芝诺悖论。
但是在量子水平上,出现了一个全新的悖论,称为量子芝诺效应。某些物理现象仅由于物质和能量的量子特性而发生,例如穿过势垒的量子隧穿或放射性衰变。为了从一种量子态进入另一种量子态,您的量子系统需要像波一样起作用:其波函数随时间扩展。
最终,在较低能量的量子态中发生缠绕的可能性将为非零。即使没有经典的途径,您也可以通过这种方式进入更加有利的状态。
但是有一种方法可以抑制这种情况:通过在波函数充分散布之前观察/测量系统。大多数物理学家将这种相互作用称为“破坏波函数”,因为您基本上是在使要测量的任何量子系统都以“类粒子”而不是“类波”起作用。但这仅仅是对正在发生的事情的一种解释,而这是一个真实的现象,与您选择的对量子物理学的解释无关。
实际情况是,您通过观察和/或测量行为来限制系统可能处于的量子状态。如果您使此测量在时间上与先前的测量过于接近,则穿隧进入所需状态的可能性将极小(甚至为零)。如果您让量子系统与环境相互作用,那么您可以抑制固有的量子效应,而仅保留经典结果作为可能性
结论是:
从一个地方到另一个地方的运动是可能的,并且由于距离,速度和时间之间明确的物理关系,我们可以准确地定量地了解运动的发生方式。是的,要覆盖从一个位置到另一位置的整个距离,您必须先覆盖该距离的一半,然后覆盖剩余距离的一半,再覆盖剩余的一半,依此类推。
但是,这样做所需的时间也减半,因此对于任何运动中的对象,在有限距离内进行运动始终只花费有限的时间。尽管对于数学家和哲学家来说,这仍然是一个有趣的练习,但不仅解决方案依赖于物理学,而且物理学家甚至将其扩展到量子现象,其中新的量子芝诺效应(不是悖论,而是对纯粹量子效应的抑制)出现。与所有科学领域一样,宇宙本身是现实行为的最终仲裁者。多亏了物理学,我们终于了解了。


