数学思维:三阶幻方
三阶幻方是最简单的幻方,又叫九宫格,是由九个数字组成的一个三行三列的矩阵(如右图示),其对角线、横行、竖列的和(即幻和)都相同。
简单的三阶幻方
题型一:已知幻和,其中的一些数字,求其他数字

正确答案:

解题思路:
规律一:中间数x3=幻和
(中间数就是在九宫格中最中心那个格子)
在这题中,幻和为36,得到中间数为12.
通过中间数,就可以得出10+12+?=36,就可以得出12下格填4.
同理 ?+4+13=36,得到19
在斜线方位 19+12+?=36 得到5.
得到这个5 还有一种
规律二: “米字”线上两头数之和=中间数X2

在这题中 19+5=12x2
利用以上2个规律就能得到所有的数字
题型二:不知幻和,只有几个数字 如图
|
A |
B |
C |
|
D |
4 |
F |
|
G |
0 |
5 |
根据规律一,幻和=中间数X3=12
得到B=8;
根据规律二,“米字”线上两头数之和=中间数X2
得到A=3
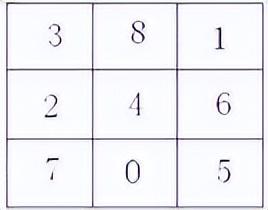
答案为:
|
3 |
8 |
1 |
|
2 |
4 |
6 |
|
7 |
0 |
5 |
题型三:已知顶角三个数 如图
|
B |
F |
E |
|
C |
A |
6 |
|
D |
0 |
5 |
规律三:顶角数X2=底边两数之和
顶角可以是任意顶角,这题中的4个顶角可以是B、E、D、5. 关键点找对底边。

顶角B对应的底边两数为0、6
顶角B对应的底边两数为0、6
得到B=3
根据规律二,B+5=2A,即3+5=2A,得到A=4
得到中间数A=4,得到幻和=中间数X3=12.其他的数就出来了。
练习一:
|
B |
5 |
E |
|
|
C |
A |
D |
|
|
8 |
F |
G |
幻和30 |
答案:
|
13 |
5 |
12 |
|
9 |
10 |
11 |
|
8 |
15 |
7 |
