用一句话说,泰勒公式就是在一点用多项式函数对一般函数的逼近。它的伟大之处就在于用已知的、简单的、容易的函数去研究未知的、复杂的、艰深的函数。当然,这里所说的已知和未知、简单和复杂都是相对而言。这种逼近有一种很好的特性,就是逼近的效果与多项式的阶数直接相关。就好比我要复制一座雕塑。我当然希望复制得越精确越好,但是更高的精度意味着更复杂的工序。如果只是看起来差不多,那我只需要用雕刻刀就可以了。但是如果要精确到毫米级,我就需要一种类似于安全系统控制组件复刻师(钥匙匠,俗称配钥匙的)用的机器。
“初次见你,我是那么讨厌你,后来的生活越来越离不开你,现在你是我心中的女皇。” ——献给美丽的泰勒公式
1. 初识泰勒公式
当我们开始上高数课或数分课大约二个月的时候,就会碰到这个令人生厌的泰勒公式,因为她太麻烦太复杂。一是她有那么多项,二是她要我们求那么多的各阶导数,三是带着一个不知道是几的中值余项,拜托,既然不知道中值是几,还弄出这个余项干么?哦,打住,别抱怨,你会慢慢爱上她的!!!
2.极限问题的核心
当 x>0 很小时,考虑 x、sin x 和 tan x 的差别有多大?回答这个问题首先要确定一个标准,就是他们之间是简单倍数关系?还是“数量级”的不同?对于初学者来说,可能还需要不少脑洞。但对于进阶者来说,马上就可以知道结果,因为当 x→0 时 sin x ~ tan x ~x,三者是等价的,不太确切地说是三者几乎相等(注意不是绝对相等)。哦,你觉得简单说明你已经差不多理解等价无穷小了。
那么进一步,把三者稍微运算一下,看看当 x>0 很小时,tan xㄧsin x 和 x^2 的差别有多大?稍有经验的同学懂得乘积情况下,因子可以用等价无穷小替换来求极限,故前者比后者小的多,因为 tan xㄧsin x=sin x (1ㄧcos x)/cos x~(x^3)/2,他比 x^2 小的多,完全不在一个“数量级”,这里所说的“数量级”其实就是 x 的次数,tan xㄧsin x 相当于 x ^3,他远远小于 x^2 。瞧,这就是阶的比较。
温馨提示: 只要两个无穷小作商,极限为0,我们就说分子是比分母高阶的无穷小。
如果你足够细心,一定发现我们把 tan xㄧsin x 转化为 (x^3)/2 了。这是最普遍的最高效的比较阶的方法,因为幂函数最容易作阶的比较了,x^3 就比 x^2 多一个 x,因此 tan xㄧsin x 是比 x^2 高阶的无穷小。
当 x→0 时,函数 f(x)~cx^k,就说 f(x) 是 x 的 k 阶无穷小,其中 c 和 k 都为非0常数。称 cx^k 是 f(x) 的主项。找到函数各因子的主项就找到了函数的极限。
温馨提示: 为了简化无穷小阶的比较,我们通常把非幂函数转化为幂函数。 极限的核心问题是无穷小阶的问题!
可以看出,函数 tan xㄧsin x 的主项是 (x^3)/2。但是找一个函数的主项不像这个例子一样简单,于是问题来了,如何找函数的主项呢?
3.泰勒公式的威力
一个函数 f(x) 在点 x0 的泰勒展开式是

其中 Rn(x)是余项,可以有两种形式,一种称为拉格朗日余项,即
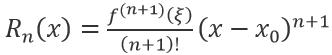
适用于展开式的误差估计,以及其他更加精细的操作,其中 ξ 介于 x 和 x0 之间。另一种称为皮亚诺余项,即
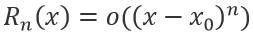
表示展开式带有这么一个误差项,大致和 (xㄧx0)^n 等价的一个无穷小。
在处理极限问题是我们更多用的是 x0=0 时的泰勒公式,也称为麦克劳林公式:
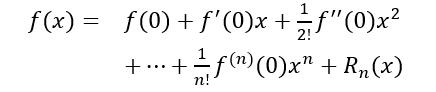
例如,sin x 和 tan x 的展开式为:

泰勒公式在求函数极限时有很高的效率,原因在于应用泰勒公式可以方便地求出函数的主项,如 sin x 和 tan x 的主项都是 x,而 tan xㄧsin x 的主项为 (x^3)/2,这是因为 tan xㄧsin x 的泰勒公展式为:
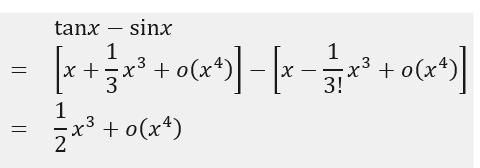
同理 sin xㄧx 的主项为 ㄧ(x^3)/6, sin xㄧx + (x^3)/6主项为 (x^5)/120。
温馨提示: 应用泰勒公式可以方便地求出函数的主项。
许多复杂的函数极限问题,应用泰勒公式都可以完美解决。
4.一个复杂的例子
本例来源于吉米多维奇习题集第1407号问题:
求 tan(sin x)ㄧsin(tan x) 的主项。
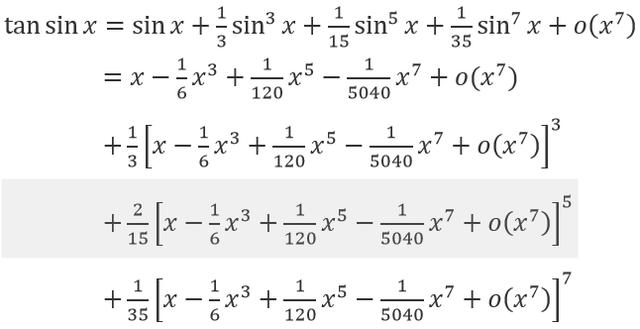
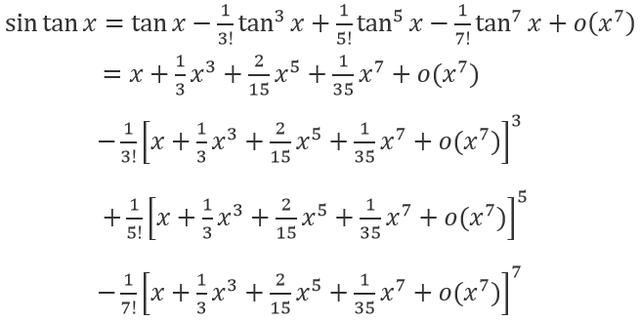

因此有下列极限
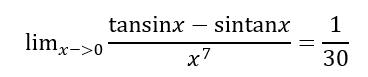
5.美丽的泰勒公式
高数大厦起极限 阶的比较破万难 敢问阶路在何方 泰勒公式若等闲
玩不转泰勒公式,请不要说“高数我能行”
玩不转泰勒公式,请不要说“我是数学人”
