绝对值的化简方法口诀绝对值化简口诀是同号得正,异号得负。
导读:新初一难点——绝对值化简,掌握不好要吃大亏
要讲绝对值的化简,首先还得铺垫一个概念——相反数,在教材上对于相反数是这么定义的:
只有符号不同的两个数,互为相反数
这个概念字数不多,却也有东西值得挖掘,
- 进一步强化学生对负数和负号的认识
- 相反数不能独立存在,而是相互依存
- 求一个数的相反数,就在这个数前面加上负号
- 求一个式子的相反数,就给这个式子加上括号,然后在括号前加一个负号
第四点举个例子,a-b+c的相反数,是-(a-b+c),然后根据需要再考虑要不要去括号。这里其实就是一个整体思想的体现。我们把a-b+c看成一个整体,这样处理就不容易出错。有很多同学都喜欢好高骛远,直接跳过一些关键步骤,然后出了错也不知道怎么检查。
就像我上一 篇文章讲到的,如何保证学生计算的100%正确率,其实就是把容易出错的方面都避免掉,不出错,就能全对。
绝对值的意义:
- 几何意义:表示数轴上的点到原点的距离
- 代数意义:正数的绝对值等于它本身;负数的绝对值等于它的相反数;0的绝对值还是0。
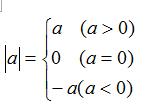
绝对值化简
绝对值化简,就是根据这两个意义来进行相关问题的处理。几何意义是数形结合思想的一种体现,代数意义主要侧重于符号、括号的运用。
例1:
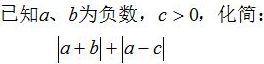
绝对值化简的一般思路,就是先确定绝对值符号内的正负,然后根据绝对值的代数意义来转化。因为a和b都是负数,所以a+b的结果也是负数,因为c是正数,a-c就是较小数减去较大数,结果必定为负。我们来看看过程:

在这个过程中,要注意几点,
- 根据绝对值的代数意义
- 相反数的表示
- 符号与括号
再来看一个结合数轴的题,
例2:数a,b,c在数轴上的位置如图:化简|b-a|-|1-c|

把数轴上的数和它们的关系整理一下:a<0,b<0,c>0,b<a,1>c,

注意我标记的两个地方,第一个注意整体思想,凡是表示一个整体的,尽量先加一个括号,然后再来去括号,不容易错,第二个标记是一种习惯,我们尽量让结果降幂、按字母表顺序排列,千万不要小看这样的一个习惯,长期注意这些细节,会让我们的思维更严谨。
例3:若ab<0,a<b,化简:
|b-a+1|-|a-b-5|
这个题结合了有理数乘法法则的运用,ab<0,说明什么?说明a、b 异号,也就是说a和b必然是一正一负,然后a<b,结合起来看,就表明a<0<b这样一个关系。

从这些绝对值化简的题目可以看出,不论题目怎么变化,涉及到的知识点只有那么几个,只要我们能够牢牢掌握知识点,不论题型怎么变,都能抽丝剥茧般把题目给分析出来。我把这种方法称为庖丁解牛法!
所以,每次学到新的知识点,请一定要记住并且理解透彻,不要在基础知识上留下任何问题,学习就会越来越轻松!
